Voronoi and Delaunay Partitioning of 2- and 3-D
Overview and Motivation
Voronoi diagrams are useful in a number of applications in graphics, crystallography, geometric modeling, among many others. They provide an algorithmic way of partitioning a region. Furthermore, they are intertwined with Delaunay triangulation which is a very useful technique for triangulating regions. Personally, my current motivation is to use Voronoi partitions and Delaunay triangulation in my soft body physics engine, documented here. It would be useful to be able to break a general 3-D model up into tetrahedrons or polyhedra algorithmically. Naturally occurring materials such as crystals have structures based on these sorts of partitions that are very stable (see the blog for more details). This article will give a general introduction to Voronoi diagrams (which I will be learning myself).
Voronoi Diagram Theory
The math behind a Voronoi diagram is very simple. Suppose we have (possibly infinitely many) "sites", which are subsets \(P_1,P_2,...\) of a metric space \(M\) (think \(\mathbb{R}^n\), some discrete space like a grid, or a manifold), with a distance function \(d\). For a set \(A \subset M\), define the distance to the set from a point \(x \in M\) to be the minimum distance to a point in \(A\): $$d(x, A) := \min\{d(x, a) | a \in A\},$$ (formally you actually use an infimum, not minimum, but the idea is the same). Then, the Voronoi cell associated with a cite \(P_k\) is the set of points: $$R_k := \{x \in M | d(x, P_k) \leq d(x, P_j), \forall j=1,2,...\}.$$ The Voronoi diagram is the tuple of all Voronoi cells and it partitions the space \(M\) into as many parts as there are sites.
To form the Voronoi diagram we can use the fact that is the dual of the Delaunay triangulation. Dual means that if we place a point at the center of every circumcircle of a triangle from Delaunay and a line between each point we get the Voronoi diagram:
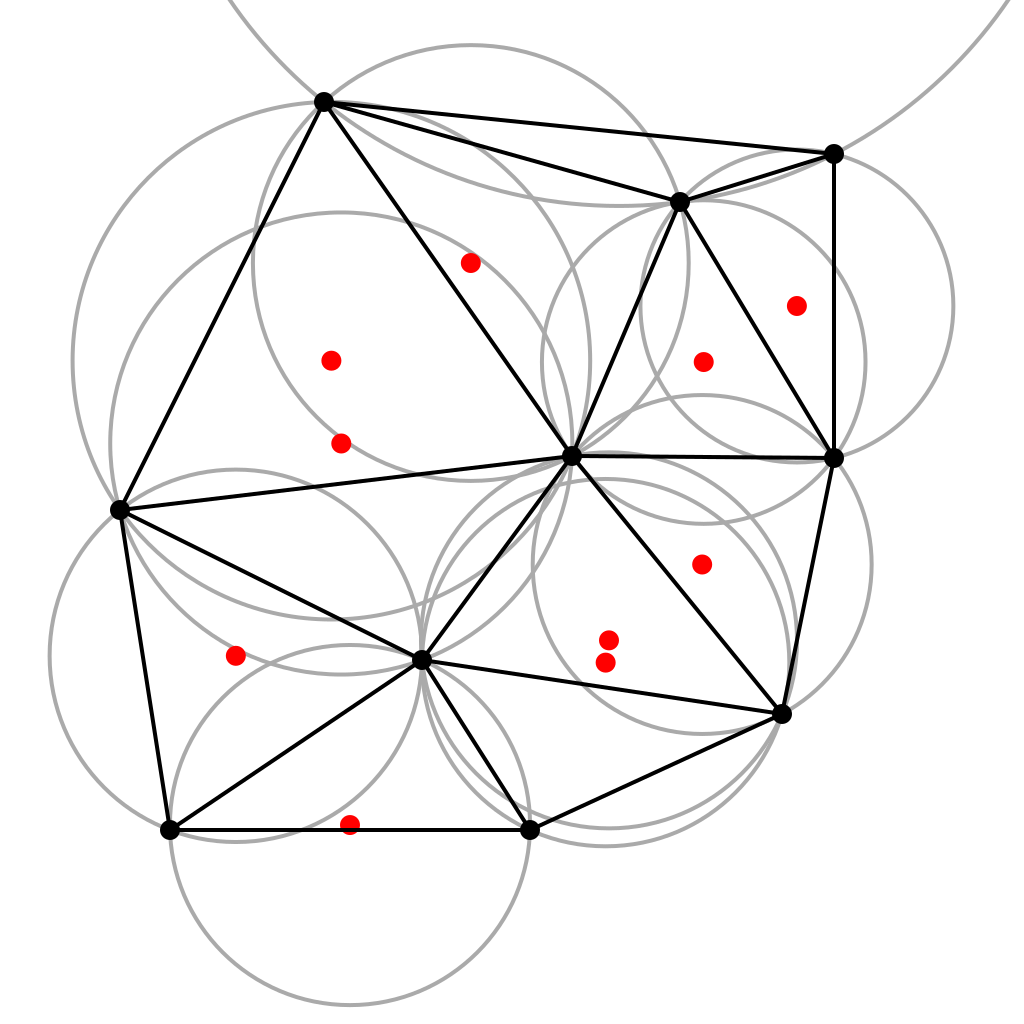
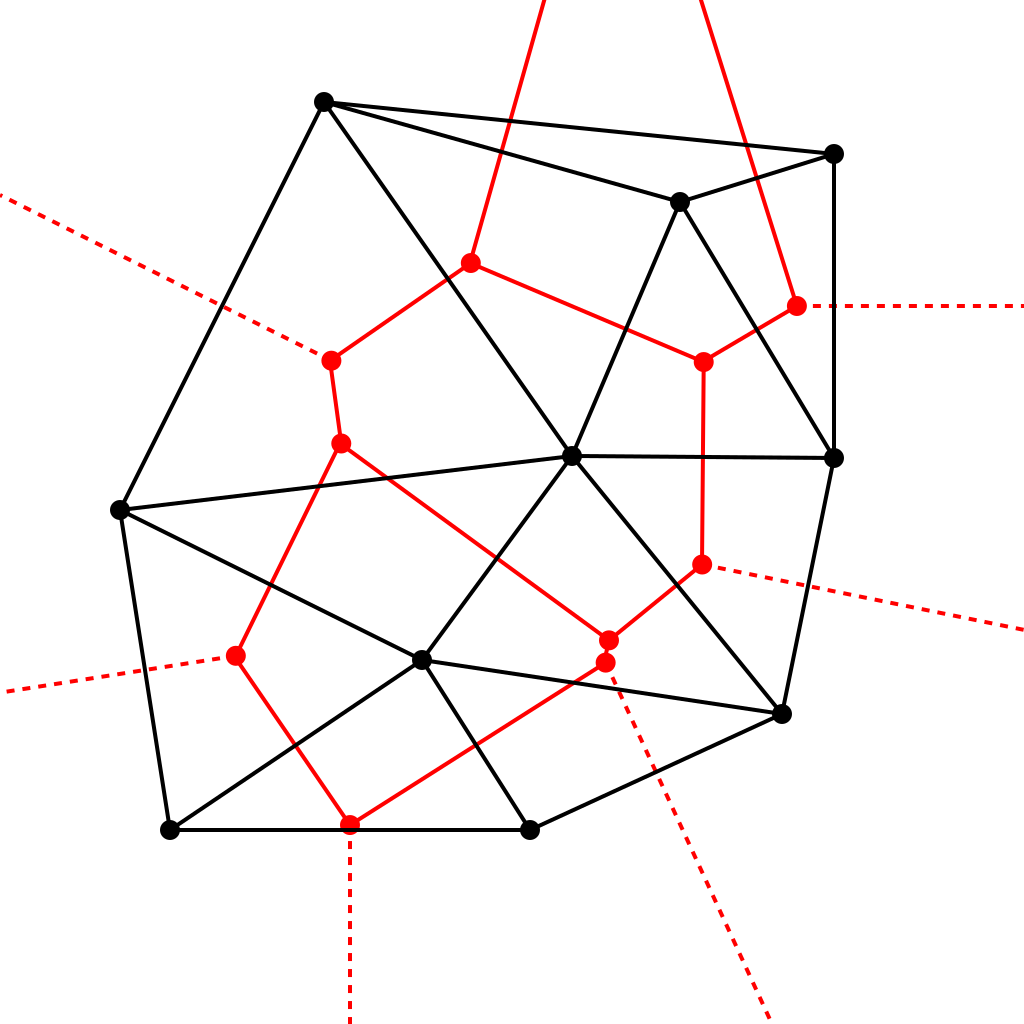
So, we can construct the Delaunay triangulation then take the dual. To construct a Delaunay triangulation most of the algorithms are based on a "flipping" principle that simple iteratively flips triangle edges as we triangulate. I am too lazy to implement these algorithms so I will use built in functions, but the algorithm is explained here.
Python Results
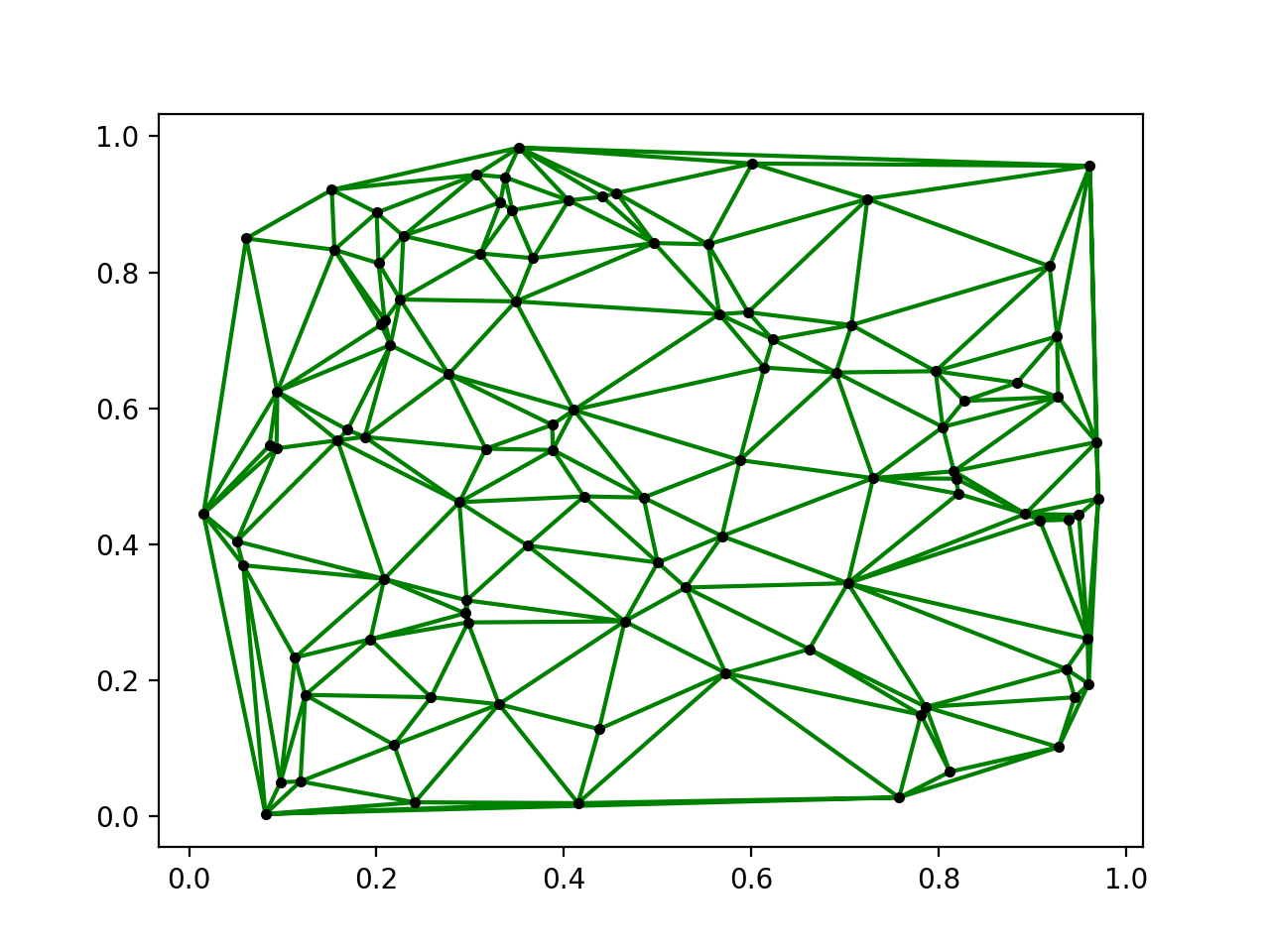
Below is some simple code in Python to get and plot a Delaunay triangulation of 100 random points:
from scipy.spatial import Delaunay
points = np.random.rand(100, 2)
tri = Delaunay(points)
plt.triplot(points[:, 0], points[:, 1], tri.simplices)
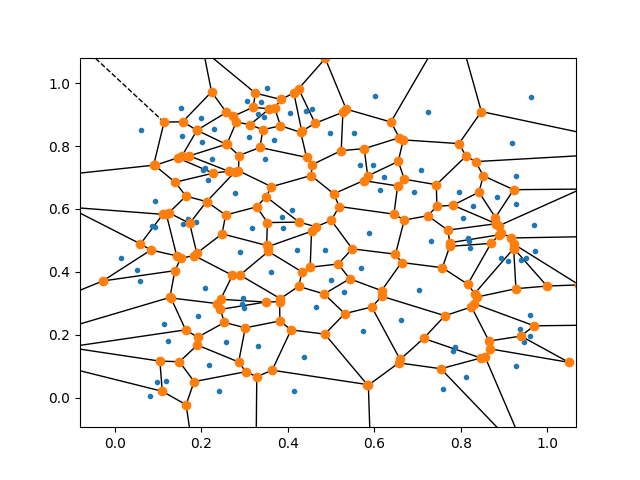
Likewise, here is some code for Voronoi partitioning:
from scipy.spatial import Voronoi, voronoi_plot_2d
vor = Voronoi(points)
voronoi_plot_2d(vor)
Here are some example results:
Here are both of the plots overlayed:
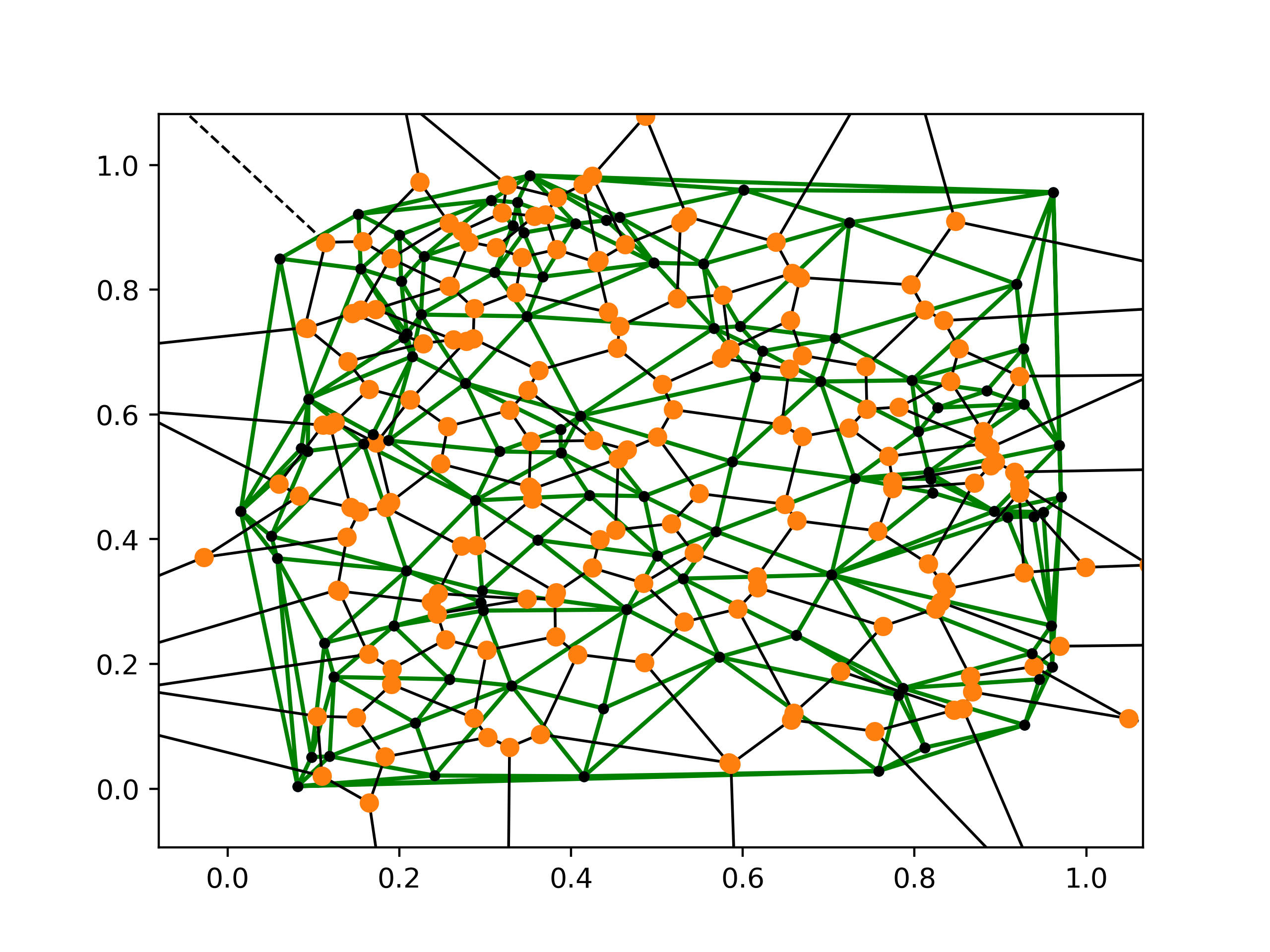
Working with 3-D Models
text here